Las figuras planas son el centro de estas dos unidades: los polígonos, pero más concretamente lo que podemos hacer con ellos y sus nombres "más específicos".
De momento en este vídeo vamos a ver la clasificación SEGÚN EL NÚMERO DE LADOS:
Con este vídeo explicamos las páginas 206 y 207; prestad atención a él y tened en cuenta que podéis verlo tantas veces como queráis y necesitéis.
Vamos a completar el vídeo con la LECTURA de los cuadros de páginas 206-207 y los ejercicios:
- Página 206: ejercicio 3
- Página 207: ejercicio 2 (lee atentamente el "Recuerda").
De estos polígonos que hemos visto, hay dos grupos que se clasifican a su vez teniendo en cuenta como son los lados y los ángulos de ellos: son los triángulos y los cuadriláteros. Tienen clasificaciones "especiales" que concreta más como son. A continuación vamos a ver dos vídeos, uno para triángulos y otro para cuadriláteros:
CLASIFICACIÓN DE TRIÁNGULOS:
CLASIFICACIÓN DE CUADRILÁTEROS:
Con estos dos vídeos, hemos visto lo relativo a las páginas: 208-209-210-211
Y lo vamos a complementar, como la vez anterior con la LECTURA COMPRENSIVA de los cuadros teóricos y los ejercicios siguientes:
Sobre triángulos: páginas 208-209: 1 y 3.
Sobre cuadriláteros: páginas 210-211: ejercicios: 2 y Razonamiento.
CIRCUNFERENCIA Y CÍRCULO:
En este caso os copio el cuadro que tenéis en el libro.
Tras leerlo muy atentamente, quiero que practiquéis los conceptos con:
- Página 212: ejercicios 1 y 3.
PÁGINA 220 EJERCICIO 1 (DEL SABER HACER)
Pasando a la UNIDAD SIGUIENTE, vamos a ver dos cosas: identificar la base y altura en triángulos y paralelogramos (es decir, cuadriláteros que tienen al menos dos lados paralelos) y cómo hallar el área de triángulos y paralelogramos.
Empezando con BASE Y ALTURA; ¿A qué nos suenan esas palabras?
- A mí, Base me suena a lo que sujeta algo, que lo mantiene "de pie".
- Y, Altura, sería algo como "lo alto que llega", cuando decimos que medimos 1,60 metros esa es nuestra altura.
En los polígonos, tanto en triángulos como en cuadriláteros va a estar relacionado.
- La base es el lado en el que "apoyamos" el polígono (cualquier lado puede ser la base dependiendo de cómo dibujemos el polígono.
- La altura es una línea perpendicular a la base desde el vértice opuesto (en algunas ocasiones coincide con otro lado, como por ejemplo en el cuadrado).
En las páginas 224 y 225 tenéis explicado esto que os he descrito yo de manera más amplia.
Quiero que, tras leerlo atentamente, hagáis los siguientes ejercicios:
Página 224 ejercicio 2.
Página 225: ejercicio 1.
Y, vamos con las áreas; solo vamos a ver la de cuadrado y rectángulo y la del triángulo.
- ÁREA DE CUADRILÁTEROS:
Teniendo en cuenta lo que hemos visto de base y altura, la fórmula general para los cuadriláteros que nos interesan hoy (rectángulo y cuadrado) es BASE x ALTURA.
Sin embargo, en el cuadrado, os lo indican un poquito diferente, ¿sabéis por qué?
En el cuadrado, la base y la altura siempre miden lo mismo, lo mismo que el lado y si recordamos la unidad de las POTENCIAS; cuando multiplico un número dos veces, formamos el cuadrado.
Es decir, si mi cuadrado tiene de lado 3 cm; la altura será 3cm tambien y para hallar el área: Base por altura, voy a multiplicar 3x3, que es lo mismo que 3 al cuadrado; o el lado al cuadrado.
- ÁREA DE TRIÁNGULOS:
Con el área de un triángulo, tenemos que ser capaces de ver que un triángulo es "medio" cuadrado o rectángulo. Así, el área será la mitad que la del cuadrilátero correspondiente. Por ello, el área lo hallamos:
Multiplicando la base por la altura y dividiendo entre dos.
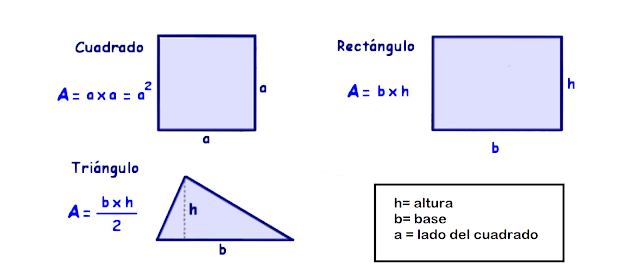
Es decir, os voy a pegar aquí una foto con las "fórmulas" para hallar las áreas:
Página 234: ejercicios 4 Y 5 (no hagáis lo que tiene que ver con círculo y circunferencia).
No hay comentarios:
Publicar un comentario